第五节 参照单位分析
参照单位分析适用于等级资料,如按疗效分为治愈、好转、无效、恶化,按反应分为-、+、++、+++,和按麻醉效果分为Ⅰ、Ⅱ、Ⅲ、Ⅳ级等的资料。
参照单位分析又称Ridit分析,常是将等级资料中例数较多的一组的分布作为一个特定的分布来计算各等级的参照单位值(R值),再参照这些R值计算各组的加权平均R值并进行假设检验。Ridit的前三个字母是Relative to an indentifieddistribution的缩写,-it是unit的字尾,故其含义是“相对于某一特定分布的单位”。由于有时将idantifieddistribution称为reference distribution,故译为参照单位 。
参照单位分析一般计算步骤如下:
1.选标准组
标准组的选择可根据各组例数多少以及所研究的问题而定。一般选例数多的组为标准组。如果各组例数相近或都较少时,可用合计数为标准组,(但若各组例数过少,则不宜用此法,可用秩和检验);若研究的是新、旧药物的疗效,则可以旧药为标准组;若研究的是患者与正常人相比较,则可选正常人为标准组。另外,标准组中的数字要求分布于各个等级,如果有的等级为0或过于少,将对计算结果产生影响。本例选辩中西组为标准组。
2.计算标准组的参照单位值,(R值)
计算前最好将各等级按由弱到强的次序排列。计算的步骤与方法是:①计算标准组各等级的1/2值②求标准组累计例数并下移一行③将①、②求得的值按各等级相加④以标准组总例数除之,即得标准组各等级的R值。
3.参照标准组的R值,计算各组的平均R值(r )
将每组中各不同疗效者例数与标准组对应的R值相乘,将乘积加总,再除以该组总例数,即为R,公式为

4.计算各组的95%可信区间进行显著性检验,R值的标准差为
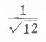

R的95%可信限为

(10.14)
按此公式算得各组的95%可信区间后,作两两间的比较,凡无重叠者即有显著差别;有重叠者则无显著差别。
例10.9 四种疗法治疗溃疡病的疗效如表10.11,试比较其疗效。
表10.11 几种疗法治疗溃疡病的疗效
| 疗效 | 例 数 | 百分比(%) | ||||||
| 西组 | 中组 | 辩中组 | 辩中西组 | 西组 | 中组 | 辩中组 | 辩中西组 | |
| 治愈 | 15 | 10 | 16 | 214 | 41.7 | 18.5 | 40.0 | 61.1 |
| 显效 | 8 | 11 | 13 | 93 | 22.2 | 20.4 | 32.5 | 26.6 |
| 好转 | 9 | 20 | 9 | 39 | 25.0 | 37.0 | 22.5 | 11.2 |
| 无效 | 4 | 13 | 2 | 4 | 11.1 | 24.1 | 5.0 | 1.1 |
| 合计 | 36 | 54 | 40 | 350 | 100.0 | 100.0 | 100.0 | 100.0 |
注:西组为单纯西药组,中组为单纯中药组,辩中组为辩证分型中草药组,辩中西组为辩证分型中西医结合组。
选辩中西组为标准组,并计算其R值如表10.12
表10.12 标准组R值计算表
| 疗效 | 例数 (1) | (1)/2 (2) | 累计例数并下移一行 (3) | (2)+(3) (4) | R值(4)/n (5) |
| 无效 | 4 | 2.0 | 0 | 2.0 | 0.006 |
| 好转 | 39 | 19.5 | 4 | 23.5 | 0.067 |
| 显效 | 93 | 46.5 | 43 | 89.5 | 0.256 |
| 治愈 | 214 | 107.0 | 136 | 243.0 | 0.694 |
N=350
R值的计算,也可用百分比进行,结果相同,见表10.13
表10.13 用百分比求R值的计算表
| 疗效 | 百分比 (1) | (1)/2 (2) | 累计例数并下移一行(3) | (2)+(3) (4) | R值(4)/n (5) |
| 无效 | 1.1 | 0.55 | 0 | 0.55 | 0.006 |
| 好转 | 11.2 | 5.60 | 1.1 | 6.70 | 0.067 |
| 显效 | 26.6 | 13.30 | 12.3 | 25.60 | 0.256 |
| 治愈 | 61.6 | 30.55 | 38.9 | 69.45 | 0.695 |
N=100.0
再计算各组的R值(加权平均参照单位值),用式(10.12),式中各符号结合本例含义是
式中∑为总和,f为各不同疗效者例数,R为与f同一疗效之标准组的R值。
标准组的R值应为0.5,可用以核对R值是否算对。
本题各组R计算如下:
R辩中西=(4×0.006+39×0.067+93×0.256+2.4×0.694)/350=0.500
R西=(4×0.006+9×0.067+8×0.256+15×0.694)/36=0.363
R中=(13×0.006+20×0.067+11×0.256+10×0.694)/54=0.207
R辩中 =(2×0.006+9×0.067+13×0.256+16×0.694)/40=0.376
将各组R值与例数代入式10.14,得各组95%可信限如下:
辩中西
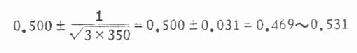
西组

中组

辩中组

将各组的95%可信区间图示如下:

图10.1 四种疗法治疗溃疡病疗效的比较(Ridit分析)
根据以上四个区间及其示意图可以看出,辩中西组的区间与其它三组都不重叠,其它三组中西组和辩中组两区间有较大重叠,而与中组都是稍有重叠,在这种情况下可作较精确的分析,因为上述R值的标准差为
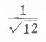
表10.14 各种等级数时的最大方差
| 等级数 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 最大方差 | 1/16 | 2/27 | 5/64 | 2/25 | 30/432 | 4/49 | 21/256 | 20/243 |
实际资料的方差都小于1/12,故用以推算得的可信区间偏大,假设检验结论比较保守。本例中组与辩中组的区间重叠部分甚少,用表10.14内数值代替1/12,则可得到更为适当的结果。该资料等级数为4,查表10.14得最大方差为5/64故标准误为

西组

中组

辩中组

这样就可以认为中组与辩中组疗效相差也是显著的,虽然这里用的仍是最大方差,但是等级为4时的最大方差,假设检验结论还是比较保守的,但比用1/12要精确些,当等级小于4时,更以查此表数值为宜。